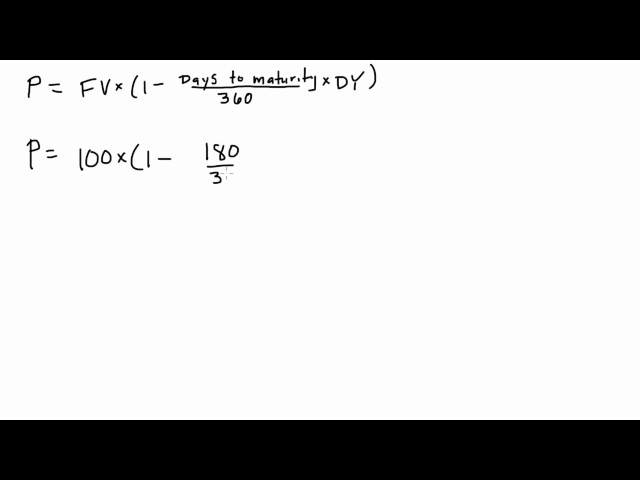Discount yield, a crucial financial metric, measures the annual return on a bond. It indicates the percentage of a bond’s face value an investor will receive as interest payments each year. For instance, a bond with a face value of $1,000 and a discount yield of 5% will pay the investor $50 in annual interest.
Understanding discount yield is essential for investors seeking fixed-income returns. It enables them to compare bonds and make informed investment decisions. Its significance lies in providing a comprehensive assessment of a bond’s profitability and risk.
The concept of discount yield traces its roots back to the early days of bond markets. Over time, its calculation method has been refined to reflect evolving market conditions. Today, it remains a cornerstone of bond analysis, guiding investors towards optimal returns.
How to Calculate Discount Yield
Discount yield, a crucial metric in bond analysis, plays a pivotal role in assessing a bond’s profitability and risk. To accurately calculate discount yield, it is essential to consider its key aspects, which encompass various dimensions of this financial concept.
- Face Value
- Coupon Rate
- Maturity Date
- Current Market Price
- Accrued Interest
- Discount
- Yield to Maturity
- Present Value
- Future Value
- Time Value of Money
Understanding these aspects is critical for investors seeking to make informed decisions about bond investments. Through examples, connections, and their relevance to the main topic, a deeper exploration of these key aspects will provide invaluable insights into the calculation and interpretation of discount yield.
Face Value
Face value, a fundamental aspect of bond analysis, forms the bedrock for calculating discount yield. It represents the principal amount or the amount borrowed by the bond issuer, which is repaid at the bond’s maturity date.
- Nominal Value: The face value is also known as the nominal value or par value of the bond.
- Maturity Amount: At maturity, the bond issuer is obligated to repay the face value to the bondholder.
- Coupon Payments: The face value serves as the base for calculating periodic coupon payments made to bondholders.
- Bond Price: The face value influences the bond’s market price, which can fluctuate based on supply and demand dynamics.
Understanding face value is crucial for investors to assess the potential return and risk associated with a bond investment. It provides a benchmark against which other bond features, such as coupon rate and yield to maturity, can be evaluated.
Coupon Rate
Coupon rate, an integral component of bond analysis, exerts a profound influence on the calculation of discount yield. It represents the annual interest payment made to bondholders, expressed as a percentage of the bond’s face value. The coupon rate plays a pivotal role in determining the overall attractiveness and risk profile of a bond.
A bond’s coupon rate directly affects its discount yield. Bonds with higher coupon rates tend to have lower discount yields, as they offer a more substantial stream of interest payments. Conversely, bonds with lower coupon rates typically have higher discount yields, as investors demand a higher return to compensate for the lower interest payments. Understanding this relationship is crucial for investors seeking to make informed decisions about bond investments.
In practice, the coupon rate is a critical factor used by investors to assess the trade-off between current income and potential capital appreciation. Bonds with higher coupon rates provide investors with a steady stream of income, making them attractive to those seeking regular cash flow. However, these bonds may offer limited potential for capital appreciation, as the higher coupon payments are already reflected in the bond’s lower market price. Conversely, bonds with lower coupon rates offer the potential for higher capital appreciation, as the lower interest payments result in a lower initial bond price. Investors may opt for these bonds if they anticipate rising interest rates in the future.
In summary, the coupon rate is a fundamental component of discount yield calculation. It serves as a key determinant of a bond’s attractiveness, risk profile, and potential return. By understanding the relationship between coupon rate and discount yield, investors can make informed decisions about bond investments, balancing their income needs with their capital appreciation goals.
Maturity Date
Maturity date, a critical aspect of bond analysis, plays a pivotal role in calculating discount yield. It signifies the specific point in time when the bond issuer is obligated to repay the face value of the bond to the bondholder. This crucial date serves as a cornerstone for determining the bond’s yield and overall attractiveness.
- Bond Term: The maturity date establishes the duration or term of the bond, indicating the period for which the investor lends funds to the issuer.
- Repayment Schedule: It determines the timing and frequency of interest payments made to the bondholder throughout the bond’s lifespan.
- Yield Calculation: The maturity date serves as a key input in calculating the bond’s yield-to-maturity (YTM), which reflects the annualized rate of return an investor can expect to earn by holding the bond until maturity.
- Discount Yield Impact: Bonds with longer maturities typically have higher discount yields compared to shorter-term bonds, as investors demand a higher return for committing their funds for an extended period.
In summary, the maturity date is an essential factor in understanding and calculating discount yield. It influences the bond’s term, repayment schedule, YTM, and ultimately its attractiveness to investors. By considering the facets discussed above, investors can make informed decisions about bond investments, balancing their risk tolerance and return expectations.
Current Market Price
Within the context of bond analysis and particularly in calculating discount yield, the current market price holds significant importance. It encapsulates the prevailing value at which a bond is traded in the secondary market, offering crucial insights into its demand and supply dynamics.
- Market Forces: The current market price reflects the interplay of supply and demand forces in the bond market. It indicates whether the bond is trading at a premium (above its face value) or at a discount (below its face value).
- Interest Rate Movements: Changes in interest rates have a direct impact on bond prices. When interest rates rise, bond prices tend to fall, making existing bonds with lower coupon rates less attractive to investors. Conversely, when interest rates fall, bond prices generally rise.
- Creditworthiness of Issuer: The creditworthiness of the bond issuer also influences the current market price. Bonds issued by entities with higher credit ratings tend to command higher market prices, as investors perceive them as less risky.
- Bond Features: Unique features of a bond, such as embedded options, can affect its market price. Bonds with call or put options, for instance, may have different market prices compared to similar bonds without such features.
In summary, the current market price of a bond is a critical factor in calculating discount yield. It reflects market sentiment, interest rate movements, issuer creditworthiness, and bond-specific features. By understanding these facets, investors can gain valuable insights into the bond’s attractiveness and potential return.
Accrued Interest
Accrued interest, a fundamental component of discount yield, represents the interest accumulated on a bond but not yet paid to the bondholder. It plays a crucial role in determining the bond’s effective yield and overall attractiveness.
- Calculation: Accrued interest is calculated based on the bond’s coupon rate and the time elapsed since the last coupon payment.
- Importance: Accrued interest is significant because it affects the effective yield of the bond. A bond purchased between coupon payment dates will include accrued interest, which adds to the investor’s total return.
- Impact on Discount Yield: Accrued interest directly influences the calculation of discount yield. Bonds with accrued interest have a higher effective yield compared to bonds without accrued interest.
- Tax Implications: In some jurisdictions, accrued interest may be subject to taxation, which can impact the investor’s overall return.
In summary, accrued interest is a critical factor in calculating discount yield and assessing the overall value of a bond investment. Understanding the facets and implications of accrued interest enables investors to make informed decisions about bond purchases and effectively manage their fixed-income portfolios.
Discount
Within the context of discount yield calculation, “discount” holds significant importance. Discount refers to the difference between a bond’s face value and its current market price. This concept is critical in determining the bond’s yield and overall attractiveness.
The discount on a bond arises due to several factors, including prevailing interest rates, creditworthiness of the issuer, and supply and demand dynamics in the bond market. When interest rates rise, the market value of existing bonds with lower coupon rates tends to decrease, resulting in a discount. Similarly, if the issuer’s credit rating declines, investors may demand a higher yield to compensate for the increased risk, leading to a discount on the bond’s market price.
Discount plays a pivotal role in calculating discount yield. A bond trading at a discount will have a higher discount yield compared to a bond trading at par or at a premium. This is because the discount effectively increases the bond’s effective yield, making it more attractive to investors seeking higher returns.
Understanding the relationship between discount and discount yield is crucial for investors in fixed-income markets. By considering the factors that influence discount, investors can make informed decisions about bond purchases and effectively manage their portfolios. This understanding enables investors to identify undervalued bonds that offer higher yields, potentially enhancing their overall returns.
Yield to Maturity
Yield to maturity (YTM) plays a critical role in the calculation of discount yield. It represents the annualized rate of return an investor can expect to earn by holding a bond until its maturity date. YTM considers the bond’s current market price, coupon payments, and the face value to be received at maturity.
The relationship between YTM and discount yield is inverse. A bond trading at a discount (below its face value) will have a higher YTM compared to a bond trading at par or at a premium. This is because the discount effectively increases the bond’s effective yield. Conversely, a bond trading at a premium (above its face value) will have a lower YTM compared to a bond trading at par or at a discount.
Understanding the relationship between YTM and discount yield is crucial for investors in fixed-income markets. By considering both metrics, investors can make informed decisions about bond purchases and effectively manage their portfolios. This understanding enables investors to identify undervalued bonds that offer higher yields or to assess the potential risks and rewards associated with investing in bonds trading at a premium.
Present Value
Present value (PV) holds a critical position in the calculation of discount yield. It represents the current worth of a future sum of money, discounted at a specified rate over a given period. Understanding the relationship between present value and discount yield is essential for investors seeking to make informed decisions in fixed-income markets.
Discount yield is calculated as the difference between the present value of a bond’s future cash flows and its current market price. The present value of these cash flows, which include coupon payments and the face value at maturity, is determined using the bond’s yield to maturity (YTM) as the discount rate. Therefore, a change in the present value of the bond’s future cash flows directly impacts its discount yield.
In practice, investors often use present value calculations to compare bonds with different maturities and coupon rates. By calculating the present value of each bond’s future cash flows and comparing it to its current market price, investors can determine which bond offers a more attractive discount yield. This analysis helps investors identify undervalued bonds that may provide higher returns or assess the potential risks and rewards associated with investing in bonds trading at a premium.
In summary, present value is a fundamental component of discount yield calculation. By understanding the relationship between present value and discount yield, investors can make informed decisions about bond purchases, effectively manage their portfolios, and identify opportunities for higher returns in fixed-income markets.
Future Value
Within the framework of discount yield calculation, future value holds significance in capturing the projected value of an investment at a specified point in the future. This concept underpins the calculation of a bond’s present value, a crucial component in determining its discount yield.
- Time Value of Money: Future value embodies the time value of money, acknowledging that the worth of a given sum changes over time due to factors such as inflation and interest earned.
- Discount Rate: The chosen discount rate, typically the bond’s yield to maturity, plays a pivotal role in determining the future value of the bond’s coupon payments and face value at maturity.
- Compounding Effect: Future value calculations incorporate the compounding effect, where interest earned is reinvested, leading to exponential growth over time.
- Investment Horizon: The length of the investment horizon, or the time until the bond’s maturity, directly influences the future value of the investment, with longer horizons generally resulting in higher future values.
In summary, future value is a fundamental concept in discount yield calculation, reflecting the time value of money, the impact of the discount rate, the compounding effect, and the investment horizon. Understanding these facets equips investors with the knowledge to accurately assess the potential returns and risks associated with bond investments, empowering them to make informed decisions in the pursuit of their financial goals.
Time Value of Money
Within the context of discount yield calculation, the time value of money (TVM) emerges as a pivotal concept, shaping the valuation of future cash flows and influencing the overall yield determination. TVM recognizes that the worth of money fluctuates over time due to factors such as inflation, interest rates, and investment opportunities.
- Present vs. Future Value: TVM acknowledges the distinction between the present value and future value of money. A dollar received today is worth more than a dollar received in the future, as it can be invested and earn interest over time.
- Compound Interest: TVM incorporates the effect of compound interest, where interest earned in a given period is added to the principal, increasing the earnings in subsequent periods.
- Discount Rate: The discount rate, typically represented by the yield to maturity of the bond, plays a crucial role in TVM calculations. This rate determines the present value of future cash flows and, consequently, the discount yield.
- Investment Horizon: The investment horizon, or the time until the bond’s maturity, directly impacts the TVM calculation. Longer investment horizons generally result in higher future values, assuming positive interest rates.
In summary, TVM is a fundamental principle in discount yield calculation. Understanding its key facets, including present vs. future value, compound interest, discount rate, and investment horizon, enables investors to accurately assess the value of future cash flows and make informed investment decisions. It serves as a cornerstone for evaluating the potential returns and risks associated with bond investments.
Frequently Asked Questions About Discount Yield Calculation
This FAQ section provides concise answers to common questions and clarifies key aspects of discount yield calculation. By addressing potential queries, we aim to enhance your understanding of this crucial concept.
Question 1: What is the formula for calculating discount yield?
Answer: Discount Yield = [(Face Value – Current Market Price) / Current Market Price] x (360 / Days to Maturity)
Question 2: How does the current market price affect discount yield?
Answer: A bond trading at a discount (below face value) will have a higher discount yield, while a bond trading at a premium (above face value) will have a lower discount yield.
Question 3: What is the relationship between discount yield and yield to maturity?
Answer: Discount yield and yield to maturity are inversely related. A bond with a higher discount yield will typically have a lower yield to maturity, and vice versa.
Question 4: How does the time to maturity impact discount yield?
Answer: Longer-term bonds generally have higher discount yields compared to shorter-term bonds, as investors demand a higher return for committing their funds for an extended period.
Question 5: What are the advantages of using discount yield to evaluate bonds?
Answer: Discount yield provides a straightforward measure of the bond’s annual return, making it easy to compare bonds with different maturities and coupon rates.
Question 6: Are there any limitations to using discount yield?
Answer: Discount yield does not consider the reinvestment of coupon payments or the potential for changes in interest rates, which can impact the bond’s overall return.
These FAQs offer a concise overview of the key concepts related to discount yield calculation. In the following sections, we will delve deeper into practical applications and explore advanced strategies for analyzing and utilizing this important metric.
Discount Yield Calculation Tips
The following tips provide practical guidance to enhance your understanding and application of discount yield calculations:
Tip 1: Accurately Determine Current Market Price: Obtain the most up-to-date market price for the bond to ensure precise calculations.
Tip 2: Consider Accrued Interest: Factor in accrued interest to capture the full value of the bond’s return.
Tip 3: Utilize a Discount Yield Calculator: Leverage online tools or spreadsheets to simplify and expedite calculations.
Tip 4: Analyze Historical and Market Data: Study historical discount yields and market trends to make informed decisions.
Tip 5: Compare Bonds with Similar Maturities: Focus on bonds with comparable maturities to ensure a meaningful comparison of discount yields.
Tip 6: Assess Creditworthiness: Evaluate the creditworthiness of the bond issuer to gauge the potential risk associated with the investment.
Tip 7: Monitor Interest Rate Movements: Stay informed about changes in interest rates, as they can significantly impact discount yields.
Tip 8: Consult a Financial Advisor: Seek professional guidance from a qualified financial advisor for personalized advice tailored to your specific investment goals.
By incorporating these tips, you can enhance the accuracy and effectiveness of your discount yield calculations, enabling you to make well-informed investment decisions.
These tips lay the foundation for successful discount yield calculation and analysis. In the concluding section, we will explore advanced strategies and techniques to further refine your understanding and empower you to harness the full potential of this important metric.
Conclusion
In summary, calculating discount yield involves understanding key concepts such as face value, coupon rate, maturity date, and present value of future cash flows. By incorporating current market prices, accrued interest, and prevailing interest rates, investors can accurately determine the annualized return offered by a bond.
The article highlighted the inverse relationship between discount yield and yield to maturity, emphasizing the impact of the bond’s market price on its overall yield. It also explored the influence of time value of money and the importance of considering the investment horizon when evaluating discount yield.
Understanding discount yield empowers investors to make informed decisions about bond investments, compare bonds with different maturities and coupon rates, and assess potential risks and returns. It remains a valuable tool for fixed-income investors seeking to maximize their returns and optimize their portfolios.